Monômio, Binômino e Trinômio
Os polinômios são formados por termos. A única operação entre os elementos de um termo é a multiplicação.
Quando um polinômio possui apenas um termo, ele é chamado de monômio.
Exemplos
a) 3x
b) 5abc
c) x2y3z4
b) 5abc
c) x2y3z4
Os chamados binômios são polinômios que possuem somente dois monômios (dois termos), separados por uma operação de soma ou subtração.
Exemplos
a) a2 - b2
b) 3x + y
c) 5ab + 3cd2
b) 3x + y
c) 5ab + 3cd2
Já os trinômios são polinômios que possuem três monômios (três termos), separados por operações de soma ou subtração.
Exemplos
a) x2 + 3x + 7
b) 3ab - 4xy - 10y
c) m3n + m2 + n4
b) 3ab - 4xy - 10y
c) m3n + m2 + n4
Operações com Polinômios
Confira abaixo exemplos das operações entre polinômios:
Adição de Polinômios
Fazemos essa operação somando os coeficientes dos termos semelhantes (mesma parte literal).
(- 7x3 + 5 x2y - xy + 4y) + (- 2x2y + 8xy - 7y)
- 7x3 + 5x2y - 2x2y - xy + 8xy + 4y - 7y
- 7x3 + 3x2y + 7xy - 3y
- 7x3 + 5x2y - 2x2y - xy + 8xy + 4y - 7y
- 7x3 + 3x2y + 7xy - 3y
Subtração de Polinômios
O sinal de menos na frente dos parênteses inverte os sinais de dentro dos parênteses. Após eliminar os parênteses, devemos juntar os termos semelhantes.
(4x2 - 5ky + 6k) - (3x - 8k)
4x2 - 5xk + 6k - 3xk + 8k
4x2 - 8xk + 14k
4x2 - 5xk + 6k - 3xk + 8k
4x2 - 8xk + 14k
Multiplicação de Polinômios
Na multiplicação devemos multiplicar termo a termo. Na multiplicação de letras iguais, repete-se e soma-se os expoentes.
(3x2 - 5x + 8) . (-2x + 1)
-6x3 + 3x2 + 10x2 - 5x - 16x + 8
-6x3 + 13x2 - 21x +8
-6x3 + 3x2 + 10x2 - 5x - 16x + 8
-6x3 + 13x2 - 21x +8
Divisão de Polinômios
Determine o quociente de 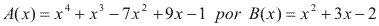 :
:
- Dividimos o termo de maior grau do dividendo pelo termo de maior grau do divisor. O resultado será um termo do quociente:
- Multiplicamos x² por B(x) e subtraímos o produto de A(x), obtendo o primeiro resto parcial:
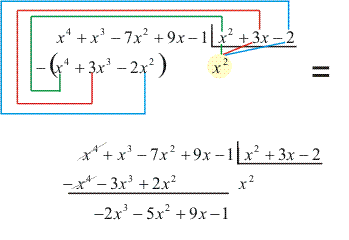
- Dividimos o termo de maior grau do primeiro resto parcial pelo termo de maior grau do divisor, e obteremos como o resultado um termo do quociente:
- Multiplicamos -2x por B(x) e subtraímos o produto do primeiro resto parcial, obtendo o segundo resto parcial:
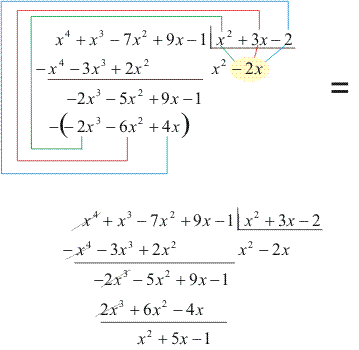
- Dividimos o termo de maior grau do segundo resto parcial pelo termo de maior grau do divisor, e obteremos como o resultado um termo do quociente:
- Multiplicamos 1 por B(x) e subtraímos o produto do segundo resto parcial:
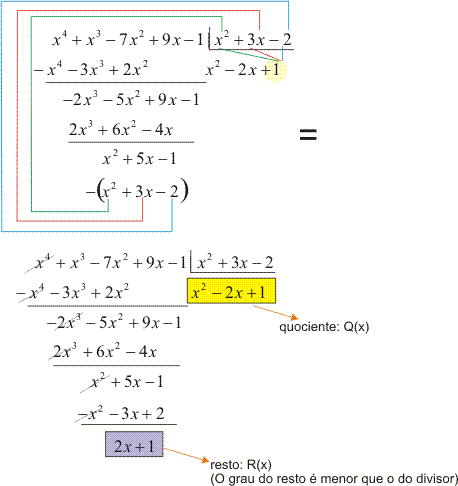
Como o grau do resto é menor que o grau do divisor, a divisão está encerrada.
Verificamos que:
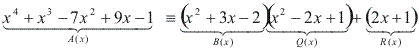
Nenhum comentário:
Postar um comentário